Understanding the Differences Between zk-STARKs and zk-SNARKs: A Guide for New Blockchain Enthusiasts
Comparing zkSNARKs and zkSTARKs: Understanding the Differences in Zero-Knowledge Proof Implementations.
This article is part of a four series introduction to Zero-Knowledge Proofs:
Introduction (The Magic of Proving Without Revealing: An Introduction to Zero-Knowledge Proofs)
Example of ZK Proofs in Go (Unlocking the Power of Zero Knowledge Proofs with Gnark and Go)
Introduction
Zero-knowledge proofs (ZKP) have been around for a while, but it wasn't until the advent of blockchain technology that their potential applications became apparent. ZKPs provide an effective way to prove knowledge of something without revealing any additional information. You can find more information on ZKP in the article here.
Overview
There are two main types of ZKP systems: zk-SNARKs and zk-STARKs.
zk-SNARK stands for Zero-Knowledge Succinct Non-Interactive Argument of Knowledge. zk-SNARKs are a type of ZKP that enables one party (the prover) to convince another party (the verifier) that they possess knowledge of a particular secret without revealing any information about the secret itself. zk-SNARKs are widely used in many blockchain applications such as privacy coins, private smart contracts, and other privacy-oriented applications.
zk-STARK stands for Zero-Knowledge Scalable Transparent Argument of Knowledge. zk-STARKs, on the other hand, are a more recent development in the world of ZKPs. Unlike zk-SNARKs, zk-STARKs do not rely on a trusted setup, making them more transparent and secure. zk-STARKs are more complex and computationally expensive than zk-SNARKs, but they offer more scalability and flexibility.
Interactive and Non-interactive what?
Interactive and non-interactive proofs are two types of proof systems used in cryptography and computer science. In simple terms, a proof system is a method for proving the validity of a statement or computation.
An interactive proof system requires communication between the prover and verifier. The prover sends a series of messages to the verifier, who then checks the messages and sends a response back to the prover. This process continues until the verifier is satisfied with the proof or decides to reject it. The main advantage of interactive proof systems is that they can be more efficient than non-interactive proof systems for certain types of problems.
A non-interactive proof system requires only a single message from the prover to the verifier. This makes it more efficient and easier to use in some scenarios, but also makes it more vulnerable to attacks.
In general, interactive proof systems are more powerful than non-interactive proof systems. They can prove more complex statements and can be more secure in some cases. However, non-interactive proof systems have their own advantages, such as being more efficient and easier to use in certain scenarios.
Explain it like I’m 5
Suppose you have a puzzle where you need to find the two numbers that add up to 10, but you can't just tell someone else what those numbers are. Instead, you need to give them a clue that they can use to check whether your solution is correct or not.
With zk-SNARKs, the clue would be something like this: "I know two numbers that add up to 10, but I can't tell you what they are. However, if you multiply them together, you'll get 21." Now the person checking your answer can multiply the two numbers together and see if they get 21. If they do, they know you solved the puzzle correctly.
However, this method has a downside. While the person checking your answer can be sure that you have the correct solution, they can't learn anything else from your clue. They don't know anything about how you arrived at your solution or what the actual numbers are.
Now, let's look at zk-STARKs. With zk-STARKs, your clue would be more like this: "I know two numbers that add up to 10, and if you follow these specific mathematical steps, you'll be able to verify my solution without me telling you what the numbers are."
In this case, the person checking your answer would use the mathematical steps you provided to verify your solution without actually learning the numbers themselves. This means they can check your answer and also learn additional information, such as how you arrived at your solution and how confident you are in your answer.
So, the main difference between zk-SNARKs and zk-STARKs is that zk-SNARKs give a single proof that can be easily checked, but without revealing much about the solution. Whereas zk-STARKs require a more complex set of mathematical steps to verify, but can reveal more information about the solution.
Explain it like I’m a pro!
Imagine you have a secret number x and a public number y, and you want to prove that you know a number z such that z is the product of x and y, without revealing x or z. In other words, you want to prove that z = x * y without revealing what x or z are.
With zk-SNARKs, you could use a so-called "quadratic arithmetic program" (QAP) to represent this computation as a set of polynomial equations, and then use those equations to generate a proof. However, as we saw in the previous example, the size of the proof depends on the size of the circuit, which can be quite large.
With zk-STARKs, on the other hand, the proof size is independent of the size of the circuit. Instead of representing the computation as a set of equations, you represent it as a sequence of constraints, which are essentially statements of the form "the difference between the values of these two polynomials at this point is equal to zero". In our example, the constraints might look something like:
x * y - z = 0(i.e., the product ofxandyequalsz)x^2 - x = 0(i.e.,xis a binary number)y^2 - y = 0(i.e.,yis a binary number)z^2 - z = 0(i.e.,zis a binary number)
You can then use a process called "low-degree extension" to convert these constraints into a set of polynomial equations, which can be evaluated much more efficiently than with zk-SNARKs. The resulting proof is then a succinct, non-interactive argument that the computation was performed correctly, without revealing any information about the secret inputs x or z.
So, as stated above, the key difference between zk-SNARKs and zk-STARKs is that zk-SNARKs are based on representing computations as a set of polynomial equations, while zk-STARKs are based on representing them as a sequence of constraints. While both approaches can be used to generate succinct, non-interactive proofs of computation, zk-STARKs have the advantage of being independent of the size of the circuit being proven, at the cost of being somewhat more complex to implement and use.
zk-SNARK in Detail
You can play with zksnarks with example code here:
The core concept behind zk-SNARKs is that they enable a prover to convince a verifier that they have knowledge of a certain piece of information, without actually revealing that information.
In order to understand how this works, it is important to understand the basics of elliptic curve cryptography. Elliptic curve cryptography is a form of public key cryptography that relies on the difficulty of solving certain mathematical problems.
In particular, elliptic curve cryptography relies on the difficulty of solving the discrete logarithm problem. The discrete logarithm problem is the problem of finding x in the equation:
y=g^x mod p
where y, g, and p are known values.
In elliptic curve cryptography, this problem is generalized to the problem of finding a point P such that:
Q=xP
where Q is a known point, P is a generator point, and x is an unknown scalar.
The basic idea behind zk-SNARKs is to use this mathematical problem to create a proof that a certain statement is true. In order to do this, the prover creates a "circuit" that represents the statement they want to prove. The circuit is essentially a graph of logical operations that takes in some inputs and produces some outputs.
The prover then maps the circuit to an elliptic curve, creating a set of equations that represent the circuit. They then use these equations to generate a proof, which is a set of values that demonstrate that the circuit is true.
The verifier can then use these values to verify the proof, without actually knowing the inputs to the circuit. This is the essence of zk-SNARKs - they allow a prover to create a proof that a certain statement is true, without revealing any information about the statement itself.
Components of the proof
The components of a zk-SNARK proof can be broken down into three parts:
Primary Inputs (or Public Inputs): These are the inputs that the verifier can see and are usually known by all parties. Examples include the transaction data, the hash of the previous block, and the public keys of the participants.
Auxiliary Inputs (or Private Inputs): These are additional inputs required to prove the validity of the computation. Examples include the private keys of the participants and any other confidential information.
Proof: This is a succinct proof that the computation was carried out correctly. It is a small, fixed-size string that can be quickly verified by the verifier. The proof is usually generated by a prover who has access to both the primary and auxiliary inputs.
The zk-SNARK proof is constructed in two phases:
Trusted Setup Phase: In this phase, a setup algorithm is run to generate the proving and verification keys. The proving key is used by the prover to generate proofs, while the verification key is used by the verifier to verify the proofs. The setup algorithm is run only once, and the keys generated are used for all subsequent proofs.
Proof Generation Phase: In this phase, the prover takes the primary and auxiliary inputs and uses them to generate the proof. This involves performing a series of mathematical calculations on the inputs to produce a statement that can be verified using the verification key. The resulting proof is then sent to the verifier along with the primary inputs.
The verifier then takes the primary inputs and the proof and uses them to verify that the computation was carried out correctly. If the verification is successful, the verifier can be sure that the prover had access to the correct inputs and that the computation was performed correctly without revealing any of the private inputs.
zk-STARK in Detail
A STARK proof system is built on top of the concept of a low-degree polynomial. A polynomial is a function of the form f(x) = a0 + a1x + a2x^2 + ... + anx^n, where ai are coefficients and n is the degree of the polynomial. A polynomial can represent a wide range of functions, including addition, multiplication, and other arithmetic operations.
A low-degree polynomial is a polynomial with a small degree that approximates the computation we want to prove. For example, if we want to prove that 2 + 2 = 4, we can represent this computation as a low-degree polynomial. One way to do this is to define a polynomial f(x) = (x - 2)(x - 2) - 4x + 8. When we evaluate this polynomial at x = 0, we get f(0) = 4, which proves that 2 + 2 = 4.
To create a STARK proof, we need to do the following steps:
Construct a polynomial that represents the computation we want to prove.
Choose a random point in the polynomial domain and evaluate the polynomial at this point.
Repeat step 2 for a number of other random points.
Use the values obtained in step 2 and 3 to construct a polynomial that approximates the original polynomial.
Publish the STARK proof.
The STARK proof is a set of points that represents the approximation polynomial. The proof can be verified by checking that the polynomial is correct at a small number of random points. This makes the proof scalable and efficient, as it only requires a small number of computations to verify the proof. Here is an example:
Unlike zk-SNARKs, zk-STARKs do not require a trusted setup phase, which makes them more transparent and easier to audit. In a trusted setup phase, a setup ceremony is performed to generate the parameters that are used in the proof system. These parameters are then used to generate the proofs, but if the setup is compromised, the entire system can be broken. With zk-STARKs, there is no need for a trusted setup phase, which makes them more resistant to attacks.
One of the drawbacks of zk-STARKs is that they require more computational resources than zk-SNARKs. This is because the proof size is larger, and the verification process requires more computations. However, with recent advancements in hardware and algorithms, zk-STARKs are becoming more feasible for real-world applications.
Overall, zk-STARKs are a promising technology for providing efficient and scalable proof systems for complex computations. They offer a high degree of transparency and auditability, making them suitable for applications that require a high level of security and trust.
Components
The components of a zk-STARK proof are different from those of a zk-SNARK proof. A zk-STARK proof consists of:
Trace: A sequence of values that represents the computation being proven. The trace is a sequence of public inputs, intermediate values, and private inputs.
Polynomial: A polynomial that represents the computation being proven. The polynomial is a high-degree polynomial whose coefficients are computed from the trace.
Prover's commitment: A commitment to the polynomial that allows the verifier to verify the correctness of the proof without knowing the polynomial.
Proof of polynomial evaluations: A proof that demonstrates that certain evaluations of the polynomial are correct. This proof is done using polynomial interpolation and is the core of the zk-STARK protocol.
In contrast to the zk-SNARK proof, the zk-STARK proof does not require a trusted setup phase, and the verification process is more transparent and efficient, making it a promising technology for large-scale blockchain applications.
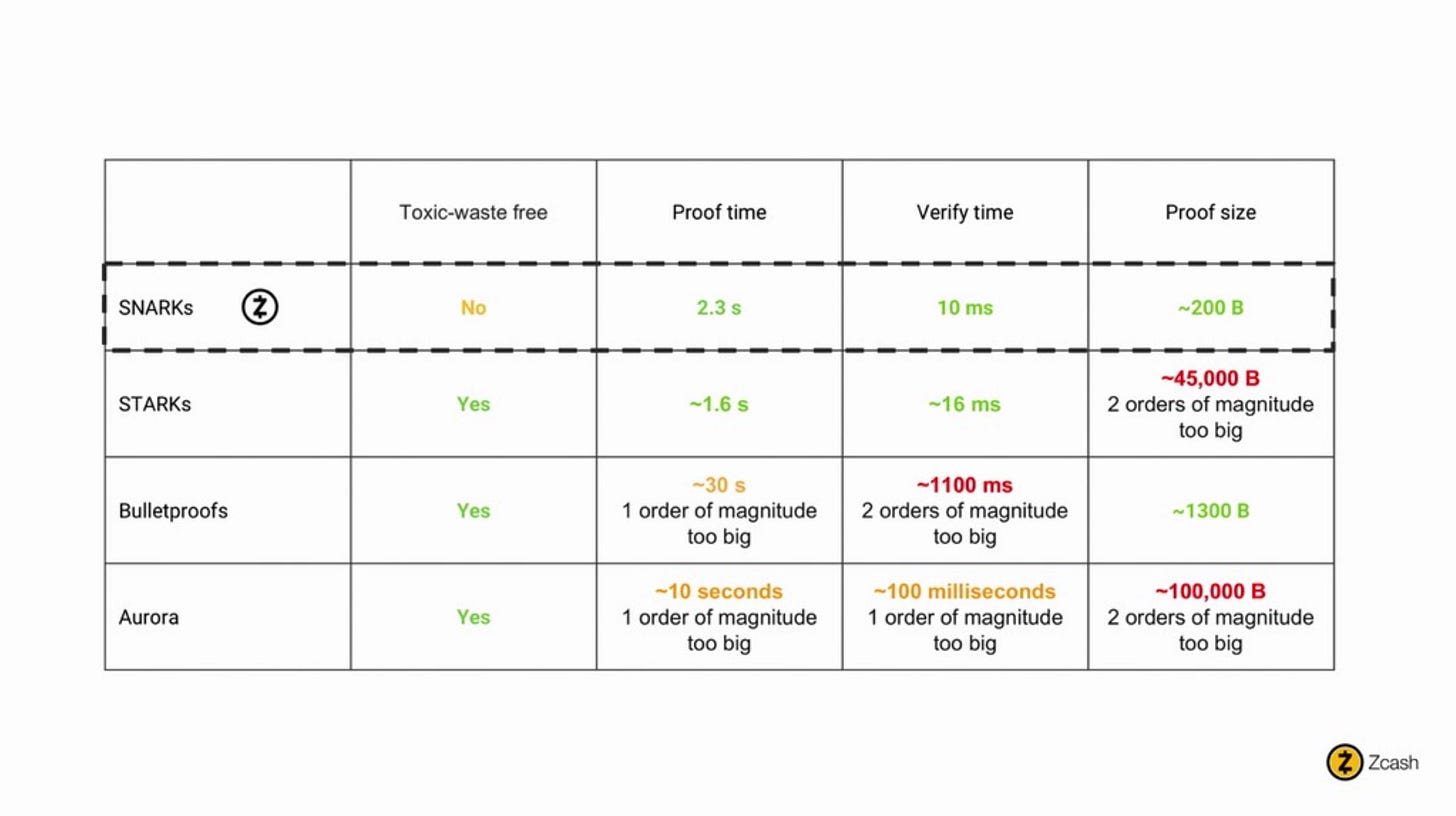
Performance Comparison
According to the awesome ZKP repo:
According to Elena Nadilinski's slides from Devcon4:
According to Zooko Wilcox's (Zcash) keynote from Devcon4:
It's worth noting that these are broad generalizations, and there are many factors that can affect the performance and security of both zkSNARKs and zkSTARKs in practice. Additionally, different use cases may require different trade-offs between proof size, verification time, and computational complexity, so it's important to carefully evaluate which technology is most appropriate for a particular application.
Conclusion
ZK-SNARKs and ZK-STARKs are two popular types of non-interactive proofs that have widespread use in blockchain technology for their ability to provide privacy and scalability.
While ZK-SNARKs and ZK-STARKs share some similarities, they differ in key ways such as their security assumptions, proof size, and efficiency. The choice between ZK-SNARKs and ZK-STARKs depends on the specific use case and the desired tradeoffs between security, proof size, and efficiency.
In the next article, we will dive deeper into Zk-Rollups and play with some code examples.