The Magic of Proving Without Revealing: An Introduction to Zero-Knowledge Proofs
A Beginner's Guide to the Mind-Bending World of Zero-Knowledge Proofs
This article is part of a four series introduction to Zero-Knowledge Proofs:
Introduction (The Magic of Proving Without Revealing: An Introduction to Zero-Knowledge Proofs)
Example of ZK Proofs in Go (Unlocking the Power of Zero Knowledge Proofs with Gnark and Go)
Introduction
Have you ever played the game "I Spy" as a kid? One person would choose an object in the room, and the other person had to guess what it was by asking yes or no questions. It was a fun way to pass the time, but what if I told you that "I Spy" could actually be a lesson in cryptography?
With Zero Knowledge Proofs, you can prove to your friend that you know what object they chose without revealing how you figured it out. It's like a secret spy mission, but with math instead of gadgets. Zero-knowledge proofs (ZKPs) are a powerful cryptographic tool that allow one party to prove to another that they possess certain knowledge, without revealing what that knowledge is. This has many useful applications, from proving identity and ownership to securing financial transactions and more. In this article, we'll explore the concept of zero-knowledge proofs and how they work, with some examples to help you understand this powerful tool.
What is a Zero Knowledge Proof?
A zero-knowledge proof is a method of proving the validity of a statement without revealing any information beyond the statement's validity. This allows one party (the prover) to prove to another party (the verifier) that they have knowledge of a particular fact or piece of information, without actually revealing that fact or information.
In other words, a zero-knowledge proof is like a magician's trick - the prover is able to prove they know something, but they don't reveal how they know it or what it is they know. This is done using complex mathematical algorithms that generate a proof that can be verified by the verifier.
Want to find an easy way to test it out? Try out with tis awesome example! ZK Crush
Explain it like I’m 5
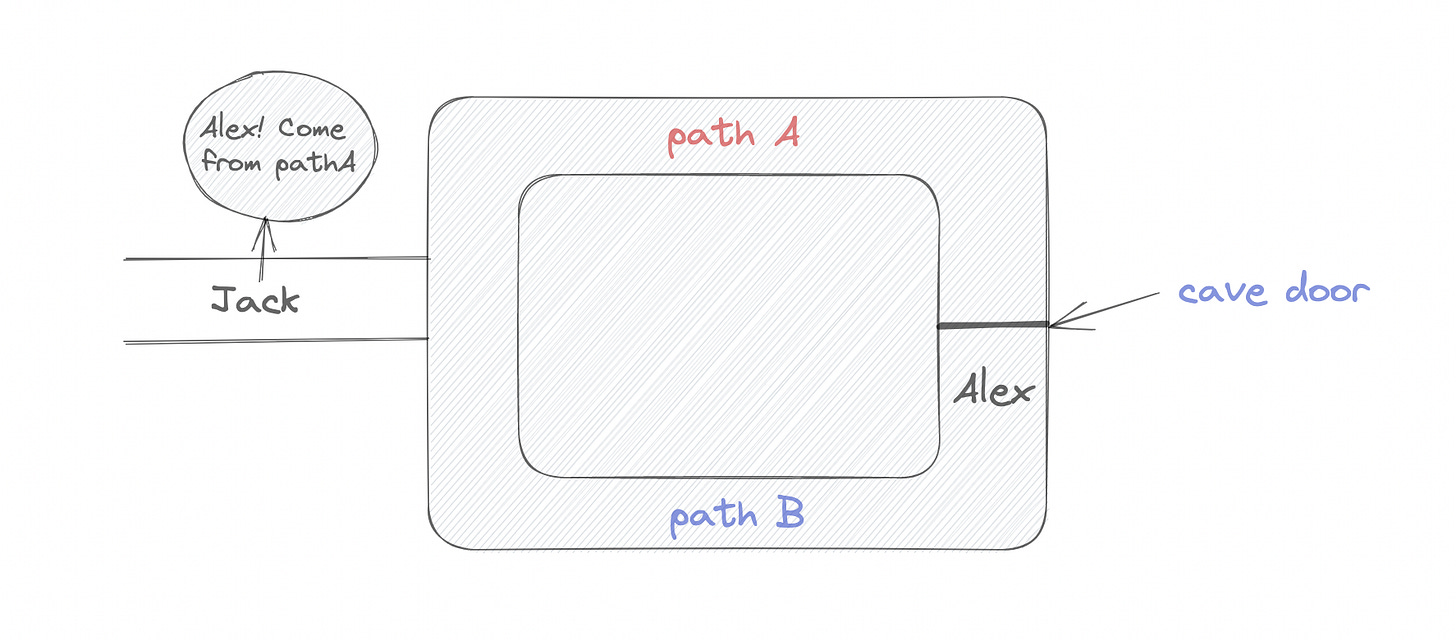
This is a story about Alex and Jack, who found a cave that has a door in the middle and this door only opens when someone knows the secret to open this door. So Alex knows the secret to open the door in the cave, and wants to prove to Jack that he knows this secret without revealing it to him.
So, Alex and Jack agree on naming both paths (let's call them paths A and B).
In the first step, Alex is inside the cave and he can choose whichever path he wants, in this particular case “A” or “B”.
After Alex choose “A”, Jack enters the cave and ask him to come outside appearing from the “B” path.
Because Alex knows the secret to open the door, he came out for the “B” path and Jack can verify that he actually knows the secret.
To summarise, the activity that Alex and Jack repeat is:
Alex enters the cave.
Alex takes a random path.
Jack enters the cave.
Jack asks Alex to come from a random path.
Alex returns using the path Jack mentioned
How do Zero Knowledge Proofs Work?
At a high level, the idea is to create a secure and private conversation between the prover and the verifier, where the prover convinces the verifier that they have the required knowledge without actually revealing it. The conversation usually consists of multiple rounds of communication, with each round involving the prover and verifier exchanging messages and performing some calculations.
During these rounds, the prover uses their knowledge to create a proof that they possess the information that the verifier is interested in. The proof is typically in the form of a mathematical statement or calculation, which the verifier can check to confirm that the prover is telling the truth without learning any additional information.
To ensure the privacy and security of the communication, zero knowledge proofs rely on complex mathematical algorithms and cryptographic techniques. These techniques are designed to ensure that the proof is valid, while preventing the prover from being able to generate a fake proof or the verifier from being able to extract any additional information beyond what is necessary.
It is hard to understand ZK proofs without concrete examples. There are multiple examples in this article, but before that, there are some conditions to be aware of.
Conditions for Zero Knowledge Proofs
Completeness: If the statement being proven is true, then an honest verifier will be convinced of its truth by an honest prover.
Soundness: If the statement being proven is false, then no cheating prover can convince an honest verifier that it is true.
Zero-knowledge: The verifier learns nothing other than the fact that the statement being proven is true. In other words, the proof does not reveal any additional information beyond the truth of the statement being proven.
The zero-knowledge condition is the most important of these three conditions. A zero-knowledge proof must not reveal any information about the secret being proved other than its truth. The verifier should not be able to learn anything else about the secret being proved, such as its value or any other related information.
Examples, examples, and more examples!
To make this more understandable, let's consider an example of a zero-knowledge proof in action with multiple examples:
Example #1: Password Verification
Suppose that you have a piece of information, such as a password or a secret phrase, and you want to prove to someone that you know it, without revealing the information itself.
You can use a zero-knowledge proof to do this as follows:
You and the verifier agree on a mathematical puzzle or problem, such as finding the factors of a large number.
You then use your knowledge of the secret information to solve the puzzle or problem. For example, you could use your knowledge of the password to compute the factors of a specially chosen number.
You present your solution to the verifier, who can verify that your solution is correct without learning anything about your secret information.
You repeat this process multiple times with different puzzles or problems, to convince the verifier that you truly know the secret information.
The verifier can be confident that you know the secret information, because you were able to solve the mathematical puzzles or problems, which is only possible if you possess the necessary knowledge. However, because the verifier only sees the solutions to the puzzles, and not the secret information itself, the proof is zero-knowledge.
In this example, the mathematical puzzle or problem serves as a stand-in for the secret information, and the solution to the puzzle serves as a proof that you know the secret. The verifier does not gain any additional knowledge beyond the fact that you know the secret, and the proof does not reveal anything about the secret information itself.
In the simple example I gave, the conditions for a zero-knowledge proof are met as follows:
Completeness: The proof is complete, because if you truly know the secret information, you will be able to solve the mathematical puzzles or problems.
Soundness: The proof is sound, because the verifier can verify that your solution to the mathematical puzzle or problem is correct, using a publicly known algorithm.
Zero-knowledge: The proof is zero-knowledge, because the verifier only learns that you know the secret information, and nothing else. The verifier does not learn anything about the secret information itself, such as the password or the factors of the number, beyond the fact that you know it. Therefore, the proof does not reveal any additional information about the secret.
Example #2: Flip a coin
Suppose you have two coins, one of which is biased to come up heads more often than tails, and the other of which is fair (i.e., comes up heads and tails with equal probability). You know which coin is which, but you want to prove to a friend that you can tell them apart, without revealing which coin is which.
Here's how you can use a zero-knowledge proof to do this:
You randomly select one of the two coins, and you flip it several times in secret.
You present the resulting sequence of coin flips to your friend, without revealing which coin you flipped.
Your friend then flips one of the two coins in front of you, and asks you to identify which coin it is.
You can then use your knowledge of the secret sequence of coin flips to identify which coin your friend flipped, without revealing which coin is which.
You repeat this process several times with different secret sequences of coin flips, to convince your friend that you can truly tell the coins apart.
In this example, the sequence of coin flips serves as a stand-in for the knowledge of which coin is biased and which is fair. By using a different secret sequence of coin flips for each round, you can prove that you truly know which coin is which, without revealing which coin is biased and which is fair.
The zero-knowledge aspect of the proof comes from the fact that your friend does not learn anything about which coin is biased and which is fair beyond the fact that you can tell them apart. Your friend does not learn which coin you flipped or which sequence of flips you used to make your determination, so the proof does not reveal any additional information about the coins themselves.
The conditions for a zero-knowledge proof are met in the coin-flipping example as follows:
Completeness: The proof is complete, because if you truly know which coin is biased and which is fair, you will be able to tell them apart based on the sequence of coin flips, and your friend will be convinced that you can do so.
Soundness: The proof is sound, because your friend can verify that you are correctly identifying the coins, by flipping one of them in front of you and checking your answer. This means that your friend can be confident that you are not simply guessing or randomly choosing a coin.
Zero-knowledge: The proof is zero-knowledge, because your friend does not learn anything about which coin is biased and which is fair beyond the fact that you can tell them apart. Your friend does not learn which coin you flipped, or which sequence of coin flips you used to make your determination. Therefore, the proof does not reveal any additional information about the coins themselves, beyond the fact that you know which is biased and which is fair.
Example #3: Guess the prime number
Imagine you have two large prime numbers, p and q, and you want to prove to a friend that you know their product n=pq, without revealing the values of p and q. How can you prove this using a zero-knowledge proof?
One way to do this is to use a variation of the RSA algorithm. Here's how it works:
You choose a random number r, and compute a new number s = r^2 mod n.
You send s to your friend, along with a claim that you know the values of p and q such that n = pq.
Your friend chooses a random number e (either 0 or 1) and sends it to you.
If e=0, you send r to your friend as a proof that you know the values of p and q. If e=1, you compute and send s/r to your friend.
Your friend can verify that you either know p and q (in the case where e=0), or that s/r is a valid square root of s mod n (in the case where e=1), without learning anything about the values of p and q themselves.
This is a zero-knowledge proof, because your friend learns nothing about p and q beyond the fact that their product is n, and your ability to prove this fact without revealing any additional information. The conditions of completeness, soundness, and zero-knowledge are met, because you can prove that you know p and q by sending r, or by computing s/r and sending that instead (if e=1), and your friend can verify that you know p and q or that s/r is a valid square root of s mod n, without learning anything else about the values of p and q.
The conditions for zero-knowledge proofs are met in the following way:
Completeness: The prover knows a prime number p and a factorization of n as p*q, and can prove this to the verifier by computing q = n/p and sending both p and q to the verifier.
Soundness: The prover cannot prove knowledge of any p and q that do not correctly factorize n, because there is no way to find a pair of numbers that correctly factorize n without knowing its prime factors.
Zero knowledge: The prover does not reveal any information about their knowledge of the prime factors of n beyond the fact that they know a prime number p and its corresponding factor q, which is already known to the verifier. Thus, the prover does not reveal any additional information about the prime factors of n.
Types of Zero Knowledge Proofs
There are several types of zero-knowledge proofs, each with their own strengths and weaknesses. Some of the most common types of zero-knowledge proofs include:
Interactive Zero Knowledge Proofs: In this type of zero-knowledge proof, the prover and the verifier interact with each other to establish the proof. The prover sends a series of messages to the verifier, who responds with challenges. The prover then uses these challenges to generate further responses until the proof is established.
Non-Interactive Zero Knowledge Proofs: This type of zero-knowledge proof requires only one message from the prover to the verifier. The proof is established without any further interaction between the two parties.
Statistical Zero Knowledge Proofs: In a statistical zero-knowledge proof, the proof is established with high probability but not with absolute certainty. This means that there is a small chance that the proof is incorrect, but this chance is so small that it is considered negligible.
Succinct Non-Interactive Argument of Knowledge (SNARKs): SNARKs are a type of zero-knowledge proof that are highly efficient and scalable. They are used in a variety of applications, including blockchain technology, machine learning, and more. Like other zero-knowledge proof systems, SNARKs allow one party (the prover) to prove to another party (the verifier) that they have knowledge of a certain piece of information, without revealing any other details about that information.
The key feature of SNARKs is that they are "succinct", meaning that the proof size is much smaller than the size of the original data being proven. This makes SNARKs highly efficient and scalable for use in a variety of applications, including blockchain technology, machine learning, and more.
Applications of Zero Knowledge Proofs
Here are some of the most common applications of ZKPs:
Identity Verification - ZKPs can be used to prove that you are who you say you are, without revealing any personal information. This has applications in online authentication, digital signatures, and access control.
Ownership Verification - ZKPs can be used to prove that you own a particular asset, without revealing any information about the asset itself. This has applications in supply chain management, intellectual property protection, and digital asset ownership.
Financial Transactions - ZKPs can be used to prove the validity of financial transactions, without revealing any information about the transaction itself. This has applications in cryptocurrency, online payments, and other digital financial transactions.
Data Privacy - ZKPs can be used to protect the privacy of sensitive data, by allowing parties to perform computations on the data without revealing the data itself. This has applications in healthcare, finance, and other industries that require the processing of sensitive data.
Elections - ZKPs can be used to ensure the integrity of elections, by allowing voters to verify that their vote was counted without revealing how they voted. This has applications in online voting and other forms of electronic voting.
Cryptography - ZKPs are a powerful tool in modern cryptography, allowing for secure communication and authentication. This has applications in military and intelligence operations, as well as in the private sector for secure messaging and other applications.
Zero Knowledge Proofs and Compliance
Zero-knowledge proofs (ZKPs) can be used in Kubernetes and regulatory compliance in a variety of ways. Here are some examples:
Kubernetes Security - ZKPs can be used to improve the security of Kubernetes clusters by providing a way to authenticate nodes without revealing any sensitive information. For example, ZKPs can be used to ensure that nodes in a Kubernetes cluster are running authorized software without revealing the specific details of the software.
Compliance Auditing - ZKPs can be used to prove compliance with regulations such as GDPR, HIPAA, and PCI DSS without revealing any sensitive information. For example, ZKPs can be used to prove that data has been encrypted and stored securely without revealing the specific details of the encryption or storage mechanism.
Access Control - ZKPs can be used to provide secure access control to Kubernetes resources without revealing any sensitive information. For example, ZKPs can be used to prove that a user has the required permissions to access a specific Kubernetes resource without revealing the specific details of those permissions.
Secure Data Sharing - ZKPs can be used to securely share data between Kubernetes clusters or between different organizations without revealing any sensitive information. For example, ZKPs can be used to prove that a specific piece of data has been shared between two parties without revealing the contents of the data.
Auditing Kubernetes Deployments - ZKPs can be used to prove that Kubernetes deployments are operating as intended without revealing the details of the deployment or the data being processed. This can help ensure that Kubernetes deployments are functioning as expected and can be useful for auditing purposes.
By allowing parties to prove things without revealing sensitive information, ZKPs can help protect against data breaches and ensure regulatory compliance. As the use of Kubernetes continues to grow, we can expect to see more and more applications of ZKPs in this area.
In the coming post, we will dive deeper into the following inshaAllah.
Example in Golang for ZK Proofs
SNARKs / STARKs
ZK Rollups